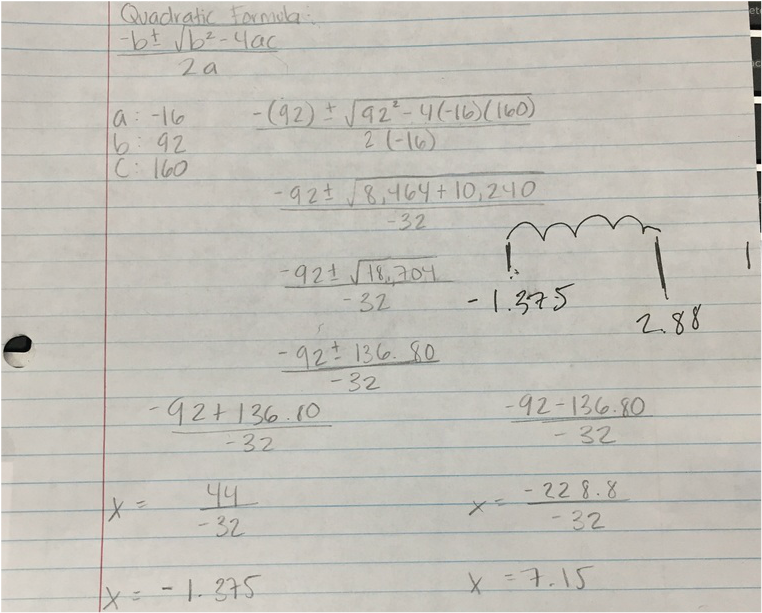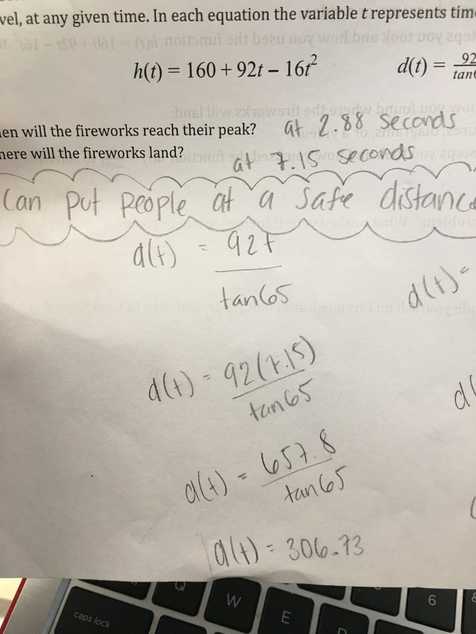Problem Statement
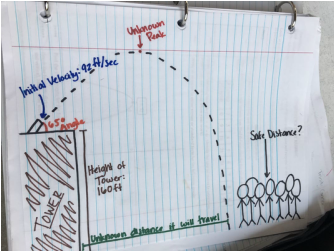
The Jefferson High junior varsity soccer team has just won the championship. To celebrate this triumph, the school will be putting on a fireworks display. The fireworks will be launched from the top of a school tower. The director isn't concerned about cost, but he wants your help with the timing mechanism that detonates the fireworks, and he's also worried about the safety of spectators.
This problem is asking you to find out when the fireworks will explode (time and height) and where they will land (time and distance) so that the school can know how far spectators need to be to be safe.
The Jefferson High junior varsity soccer team has just won the championship. To celebrate this triumph, the school will be putting on a fireworks display. The fireworks will be launched from the top of a school tower. The director isn't concerned about cost, but he wants your help with the timing mechanism that detonates the fireworks, and he's also worried about the safety of spectators.
This problem is asking you to find out when the fireworks will explode (time and height) and where they will land (time and distance) so that the school can know how far spectators need to be to be safe.
Process and Solution
The first thing we did was come up with a list of questions we needed the answers to, to solve the problem:
-What is the horizontal distance the fireworks will travel?
-What do the variables stand for?
-Is t the number of fireworks?
-How long will the fireworks take to reach the peak(vertex)?
-Where will the fireworks land?
-What is a safe distance for spectators?
My initial attempt at solving this problem was to make a graph with all the information we knew and what we needed to know, it was like a visual representation of the problem.
The first thing we did was come up with a list of questions we needed the answers to, to solve the problem:
-What is the horizontal distance the fireworks will travel?
-What do the variables stand for?
-Is t the number of fireworks?
-How long will the fireworks take to reach the peak(vertex)?
-Where will the fireworks land?
-What is a safe distance for spectators?
My initial attempt at solving this problem was to make a graph with all the information we knew and what we needed to know, it was like a visual representation of the problem.
Initial Attempt
When I started to try to solve the problem I kept trying to solve for t but that was kind of a challenge because I didn't know how to multiply by tan 65 or what the rule was when you square rooted variables and I totally did not even think about putting into standard form, I didn't even know what standard form was. Honestly in the beginning of the problem my group and I had no idea what to do.
When I started to try to solve the problem I kept trying to solve for t but that was kind of a challenge because I didn't know how to multiply by tan 65 or what the rule was when you square rooted variables and I totally did not even think about putting into standard form, I didn't even know what standard form was. Honestly in the beginning of the problem my group and I had no idea what to do.
Finding where the fireworks will land
To find where the fireworks would land (or touch the x axis) I looked at the formula h(t)=160+92t-16t^2 I wanted make it something more familiar and make it easier to plug into the quadratic function so I rearanged it to make it h(t)=-16t^2+92t+160. "t"= time so when it's h(t) that means height (h) at a certain time (t) and when it's d(t) that's distance (d) at a certain time (t). I used the quadratic formula to solve for the x intercepts.
To find where the fireworks would land (or touch the x axis) I looked at the formula h(t)=160+92t-16t^2 I wanted make it something more familiar and make it easier to plug into the quadratic function so I rearanged it to make it h(t)=-16t^2+92t+160. "t"= time so when it's h(t) that means height (h) at a certain time (t) and when it's d(t) that's distance (d) at a certain time (t). I used the quadratic formula to solve for the x intercepts.
The quadratic formula gave me x=-1.375 and x=7.15 so I know that the fireworks land after 7.15 seconds. But I don't know the vertex or where the spectators can stand to be a safe distance away.
To find the distance in feet I plug the x intercept 7.15 in for t in the formula d(t)=92t over tan65.
I got d(t)=306.73feet
So you can put spectators anywhere after 306.73 feet and they will be safe.
To find the distance in feet I plug the x intercept 7.15 in for t in the formula d(t)=92t over tan65.
I got d(t)=306.73feet
So you can put spectators anywhere after 306.73 feet and they will be safe.
Finding the peak or vertex
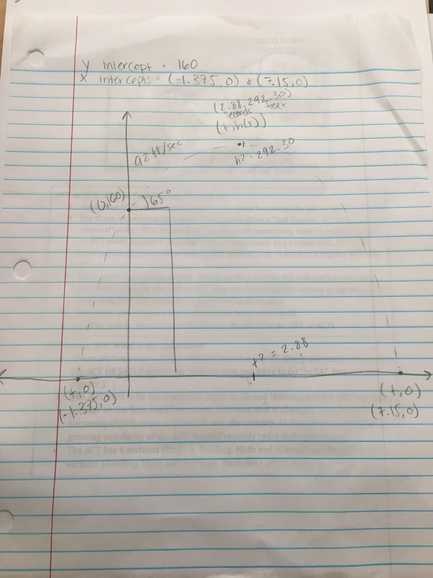
So now to find the middle point I added the x intercepts to find the total difference. 1.375+7.15=8.525
I divided that distance by 2. 8.525/2=4.25
Then I added that distance to one of the x intercepts to find the middle point between the 2 x intercepts. -1.375+4.25=2.88
So 2.88 is the x value for the vertex because it is in the middle of the two x intercepts and to find y I just plugged it into the formula h(t)=160+92t-16t^2 and I got -132.64+264.96+160=292.32ft so the vertex is (2.88,292.32), the x intercepts are (7.15,0) & (-1.375,0) and the y intercept (0,160)
So now to find the middle point I added the x intercepts to find the total difference. 1.375+7.15=8.525
I divided that distance by 2. 8.525/2=4.25
Then I added that distance to one of the x intercepts to find the middle point between the 2 x intercepts. -1.375+4.25=2.88
So 2.88 is the x value for the vertex because it is in the middle of the two x intercepts and to find y I just plugged it into the formula h(t)=160+92t-16t^2 and I got -132.64+264.96+160=292.32ft so the vertex is (2.88,292.32), the x intercepts are (7.15,0) & (-1.375,0) and the y intercept (0,160)
Problem Evaluation
I really liked this problem because I learned a lot trying to solve this problem. I feel like it definitely pushed my thinking because I can memorize the steps to solve but sometimes people would ask me why things were the way that they were and that pushed my thinking a lot. This problem really helped me focus and remember some of the more basic aspects of math, like manipulating formulas and solving for a variable.
I really liked this problem because I learned a lot trying to solve this problem. I feel like it definitely pushed my thinking because I can memorize the steps to solve but sometimes people would ask me why things were the way that they were and that pushed my thinking a lot. This problem really helped me focus and remember some of the more basic aspects of math, like manipulating formulas and solving for a variable.
Self Evaluation
I think I should get an A because I think for most of the unit I was focused and engaged during math class, and I worked really hard to make sure I was understanding. I also think I was challenged by this unit and I was able to work with other people with this problem, either by asking or answering questions or helping other people understand the problem.
I think I should get an A because I think for most of the unit I was focused and engaged during math class, and I worked really hard to make sure I was understanding. I also think I was challenged by this unit and I was able to work with other people with this problem, either by asking or answering questions or helping other people understand the problem.
Edits
-Made pictures smaller
-Made titles bigger
-Added spaces
-Explained what "t" is
-Re uploaded images so they can be viewed
-Put the diagram
P.S. The images are being weird about letting me change the size, so that's why they are all different sizes.
-Made pictures smaller
-Made titles bigger
-Added spaces
-Explained what "t" is
-Re uploaded images so they can be viewed
-Put the diagram
P.S. The images are being weird about letting me change the size, so that's why they are all different sizes.