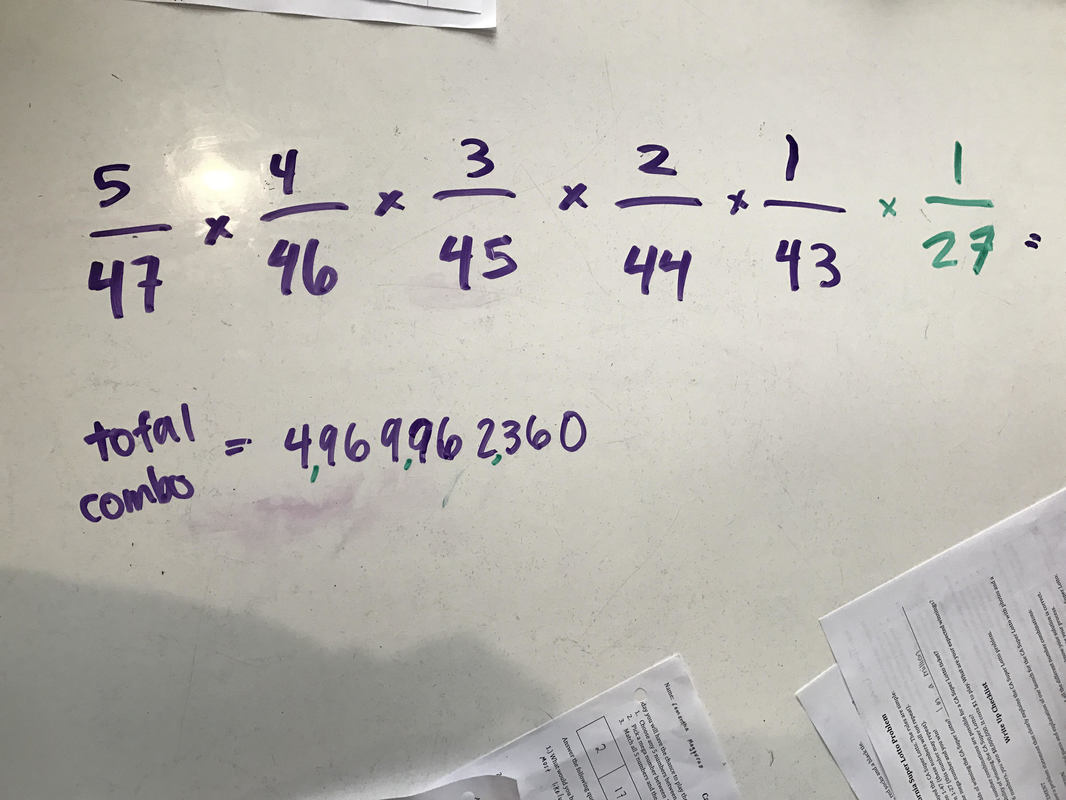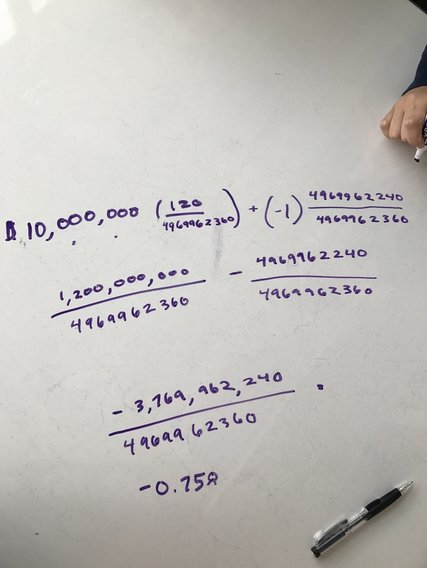Problem Statement:
In the beginning of this semester we made a guess about the odds of winning the lottery, my guess was 1 in a million people win the lottery. First this problem was asking us to figure out how many different lottery tickets or number combinations there could be, like all the different combinations of the 5 numbers and the mega numbers you could choose. Then it asked us what the real probability of winning the lottery was with the actual numbers and calculations. The third part of the problem was to figure out what the expected winnings would be if you won.
In the beginning of this semester we made a guess about the odds of winning the lottery, my guess was 1 in a million people win the lottery. First this problem was asking us to figure out how many different lottery tickets or number combinations there could be, like all the different combinations of the 5 numbers and the mega numbers you could choose. Then it asked us what the real probability of winning the lottery was with the actual numbers and calculations. The third part of the problem was to figure out what the expected winnings would be if you won.
Process and Solutions:
When we started this unit we talked about the CA Super Lottery and then we played in our class. No one won, I think the highest one person got was that they matched 3 numbers. My initial guess for the odds of winning the lottery was 1 in a million.
When we started this unit we talked about the CA Super Lottery and then we played in our class. No one won, I think the highest one person got was that they matched 3 numbers. My initial guess for the odds of winning the lottery was 1 in a million.
|
None of my numbers hit. After we all lost at the lottery we looked at how to calculate probability. Some notes we took were:
-Probability: A value between 0 and 1 assigned to a random outcome -Sample Space: Set of all possible outcomes (Ex: rolling a die, sample space=6) -Event: A successful outcome (Ex: rolling a 6=1) -P(A): Probability of A (Probability of event A occurring) P(A)= #of successful outcomes (events)/total outcomes (sample space) Ex: Rolling a 6/ Rolling a die= 1/6 After we learned those terms we looked at the 4 different types of probability: basic probability=P(A), complements= P(Ac), intersections P(A and B), and unions= P(AUB). We used these skills to transition into Independent vs. Dependent Events, Conditional Probability, and finally Expected Value. Once we learned all of these things we had all the tools we needed to solve for the CA Lottery Problem (see below for worksheets). |
Solving Question 1and 2: How many different number combinations are possible for a CA Super Lotto ticket? and What is the probability of winning the CA Super Lotto?
We started by thinking about our numbers, we knew we had to choose 5 numbers from 1-47 that couldn't repeat* and 1 number from 1-27 that could repeat. We first thought that we would just have to multiply all the sample spaces together (to the left). And we had to take one away from the sample space each time because the numbers you choose can't be repeated.
We started by thinking about our numbers, we knew we had to choose 5 numbers from 1-47 that couldn't repeat* and 1 number from 1-27 that could repeat. We first thought that we would just have to multiply all the sample spaces together (to the left). And we had to take one away from the sample space each time because the numbers you choose can't be repeated.
|
But then we realized that you can have any combination of 5 numbers and then once you chose one it decreases to 4, then 3 and so on until you get to one (to the right).Then for the mega number you just leave it as 1/27 because you pick any 1 number and it can repeat. So for the total combinations we got 4,969,962,360. And the probability of winning the lottery is 120/4,969,962,360, Which simplified is 1/41,416,353. Which means that 1 in every 41,416,353 people win the lottery, which is also 0%.
|
Solving Question 3: If you match all 6 numbers you win $8,000,000, it costs $1 to play, what are your expected winnings?
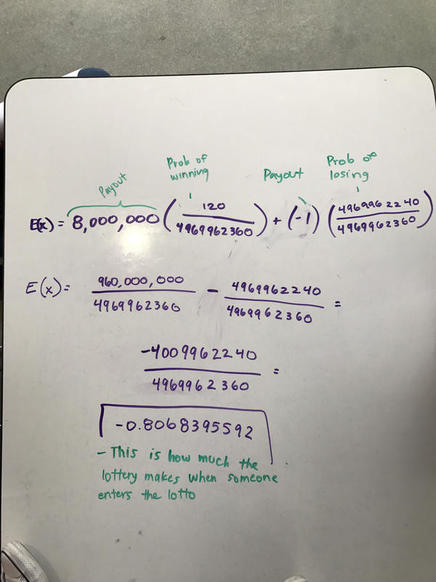
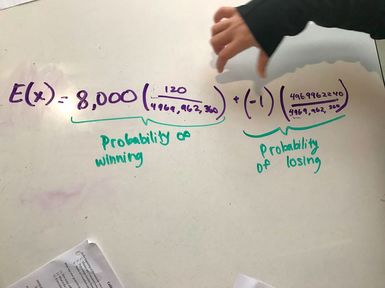
To answer this question we just plugged everything into the expected value formula. Which is the payout (the probability of winning) + payout (probability of loosing). After that you just solve. Our first answer we got was -0.9 which would mean that for every $1 someone puts into the lottery (buys a ticket) the lottery profits 90 cents of that. But those calculations were wrong because as you can see in the image in the right we calculated the payout as $8,000 instead of $8,000,000. When we calculated it again we got -0.806 which means that for every dollar someone spends on the lottery they get 80 cents.
To answer this question we just plugged everything into the expected value formula. Which is the payout (the probability of winning) + payout (probability of loosing). After that you just solve. Our first answer we got was -0.9 which would mean that for every $1 someone puts into the lottery (buys a ticket) the lottery profits 90 cents of that. But those calculations were wrong because as you can see in the image in the right we calculated the payout as $8,000 instead of $8,000,000. When we calculated it again we got -0.806 which means that for every dollar someone spends on the lottery they get 80 cents.
|
Problem Evaluation:
I liked this problem because I thought it was something that really connected to the real world. What pushed my thinking was the challenge option (below) because we started at .80 and had to get it down to .0 with out having to calculate for each million we added. I think I got the most out of question #3 and the challenge option because now I know how to calculate when the reward gets high enough that the lotto doesn't profit, so I think this problem wasn't just like normal problems when you're like okay when am I ever going to use this in real life? I think this problem had a really good real world connection so for me that made it more relevant. |
Self Evaluation:
If I were to grade myself on this unit I would give myself and A+, because I think compared to the last unit my group work has really improved and I think I met my goals from my POL with this unit. Also I've turned in everything on time and stayed focused in class like 90% of the time. Also I really liked this problem so I think I did put a lot of effort into the unit. And my DP is pretty thorough I would say.
If I were to grade myself on this unit I would give myself and A+, because I think compared to the last unit my group work has really improved and I think I met my goals from my POL with this unit. Also I've turned in everything on time and stayed focused in class like 90% of the time. Also I really liked this problem so I think I did put a lot of effort into the unit. And my DP is pretty thorough I would say.
Challenge Option:
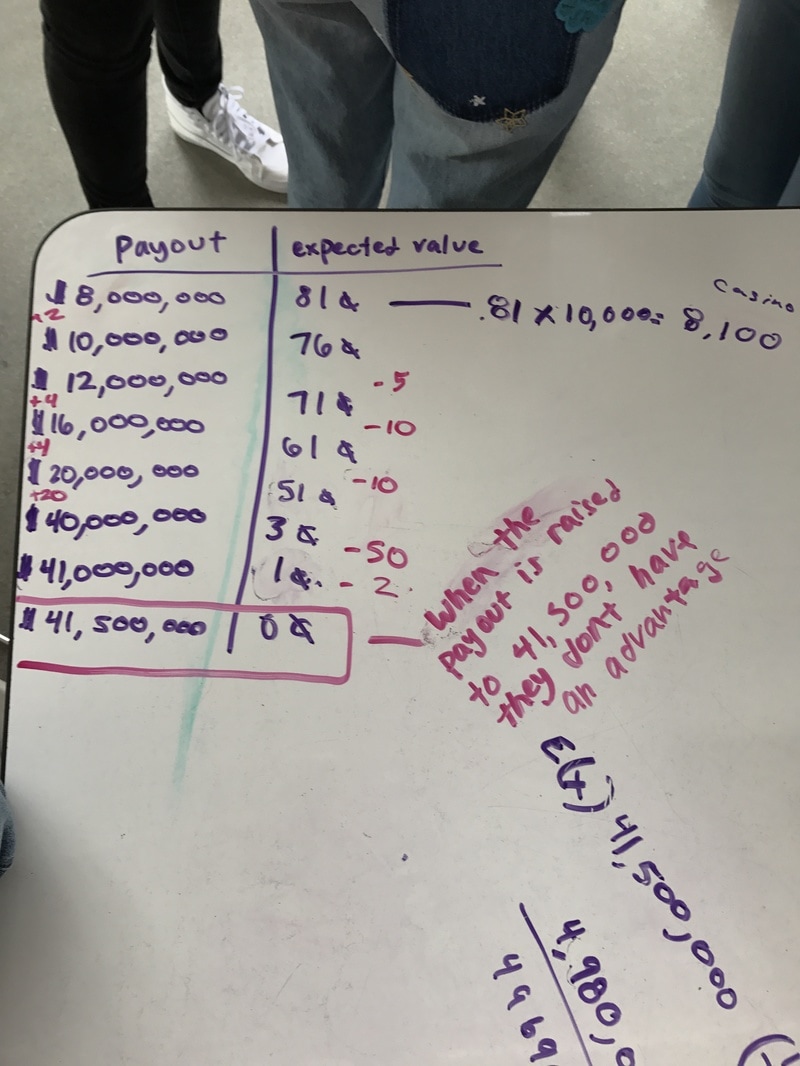
The challenge option was to find how much the reward would have to be for it to be profitable for you to enter the lottery. So what that means is at what payout will the expected value be equal to 0 instead of -.80. We started out by adding 2,000,000 to the 8,000,000 and calculating for 10,000,000 that only got us down to -.76 so we made a table using that pattern and we thought that if we calculated the expected value for a payout of 40,000,000 we would get -.01, but we actually got -0.03. So we added another million and got -0.01 which was so close, so we didn't want to add another million because then it would've been positive so we tried calculating for 41,500,000 and we got -.00 :) which is what we wanted. So that means that when the lottery's payout reached 41,500,000 it's a better idea for you to invest your money in it then so that the lottery isn't profiting 80% of what you put in.
The challenge option was to find how much the reward would have to be for it to be profitable for you to enter the lottery. So what that means is at what payout will the expected value be equal to 0 instead of -.80. We started out by adding 2,000,000 to the 8,000,000 and calculating for 10,000,000 that only got us down to -.76 so we made a table using that pattern and we thought that if we calculated the expected value for a payout of 40,000,000 we would get -.01, but we actually got -0.03. So we added another million and got -0.01 which was so close, so we didn't want to add another million because then it would've been positive so we tried calculating for 41,500,000 and we got -.00 :) which is what we wanted. So that means that when the lottery's payout reached 41,500,000 it's a better idea for you to invest your money in it then so that the lottery isn't profiting 80% of what you put in.
|
|
|
Worksheets
Edits:
-Made the worksheet pictures bigger
-Added spaces after each probability note
-Made the text bigger
-Added the challenge option
-Made the worksheet pictures bigger
-Added spaces after each probability note
-Made the text bigger
-Added the challenge option